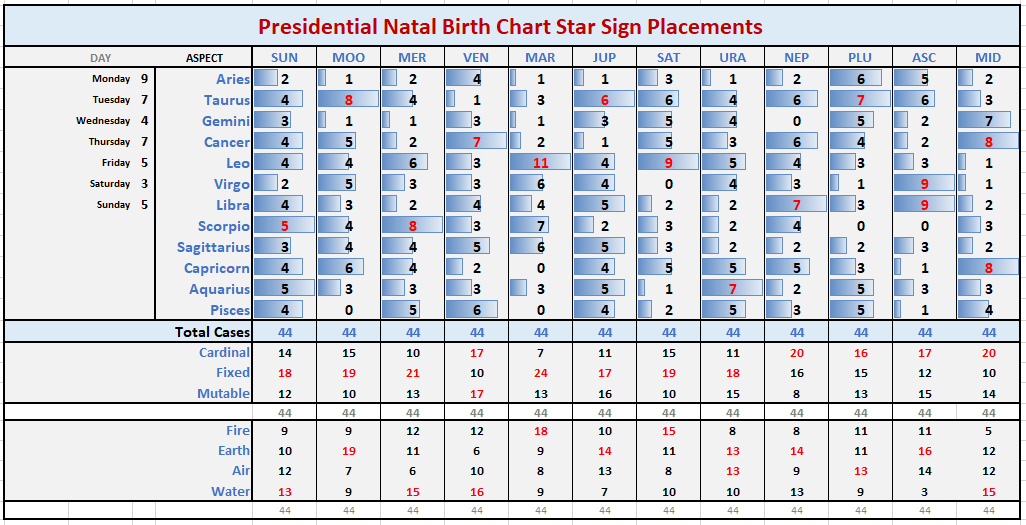
The Sacred Geometry at work in the Birth Stars
of the Presidents and their Destine relationship to the White House
Below is just a sample of a few US Presidents who stars at their birth were observed forming geometric shapes that took them straight to the White House. We will add more Presidents of past as we find them. For now, let this work serve to illustrate how using the stars to make these parallels we are hopeful will support how they can trusted in cases of missing persons.
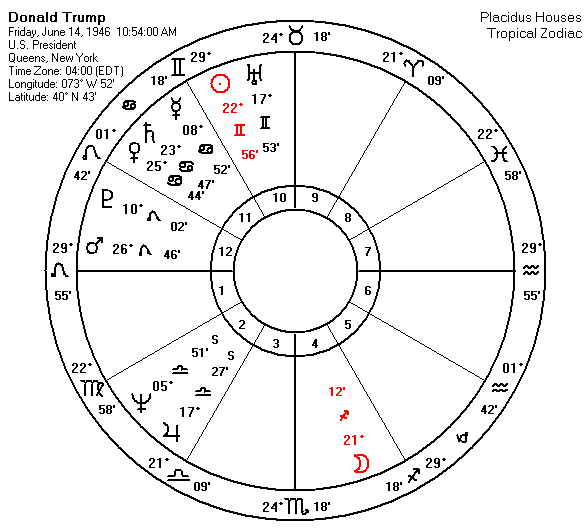
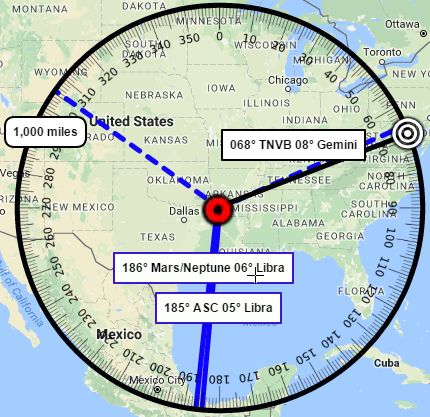
45th President Donald J. Trump
It is 210 Miles from the Jamaica Queens, New York to the White House. Trump's has a "fantastic" Sun/ Uranus conjunction in Triangle to an "amazing" Jupiter in Libra. Keep in mind the its sign symbol is the scales of justice. It's really a "terrific' aspect folks. Really terrific. Joking aside folks, Trumps' stars promise that he will not to be the "disaster" some of the Americans thinks he will be.
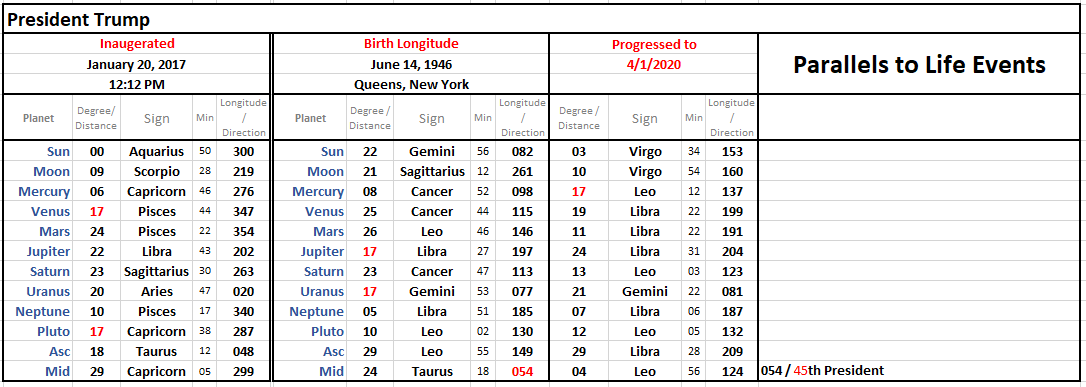
Trump was born destine for the White House just as the previous illustrated men here have been destine for the White House from the pattern of their Stars. Here is how it works, for Trump. He has,
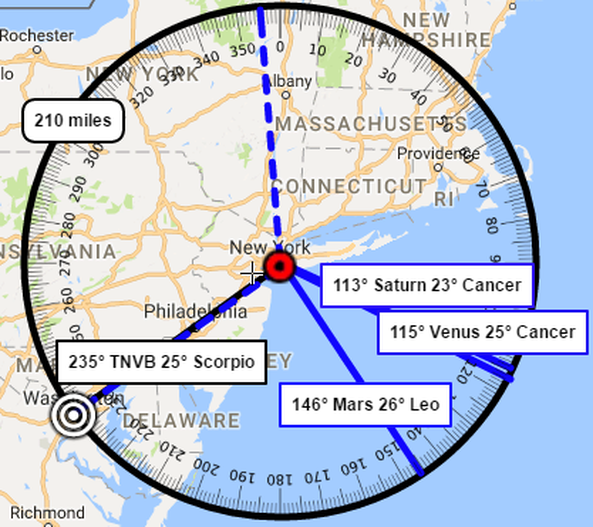
In the Matter of DIRECTION
The compass bearing from Jamaica Queens to the White House is 235° which is also expressed as 25° of Scorpio.
- 082° - Sun 22° of Gemini
- 077° - Uranus 17° of Gemini
- 197° - Jupiter 17° of Libra
In the Matter of DIRECTION
The compass bearing from Jamaica Queens to the White House is 235° which is also expressed as 25° of Scorpio.
- Trumps' natal Venus at 25° of Pisces conjoins his Saturn at 23° of Cancer both form a TRINE to this point, while his
- Ascendant at 17° in Leo, Squared this point., by 7 degrees, and his rising
- Mars at 26° in Leo, also Squared this point, and that Square is doing exactly what a Square does, cause tension.
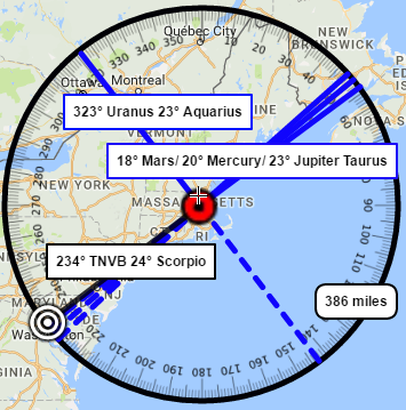
44th President
44th President john F. Kennedy
|
In the Matter of Direction
The compass bearing from Beals Street to the White House is 234° which is also expressed as 24° of Scorpio.
In the Matter of Distance
It was 386 Miles from point of birth 83 Beals Street, Mass to Washington DC. The sames planets involved in form part of the T-Square that brought JKF o the White House are the same planets whose measurements in total degrees of celestial longitude of 053° and 323° when add, sum to 376, fall just 10 miles short of 386 Crow Flies Miles.
But if your picky like me, than you can always sight JFK's natal Sun at 7° Gemini forming a semi-sextile to his natal Pluto at 3° Cancer and add those figures to the 376 to get to the 386 Miles from Beals St to DC. And I can do this because JFK's Sun conjoins Uranus and while his Pluto conjoins Venus in the natal birth map of the United States erected for July 4, 1776. |
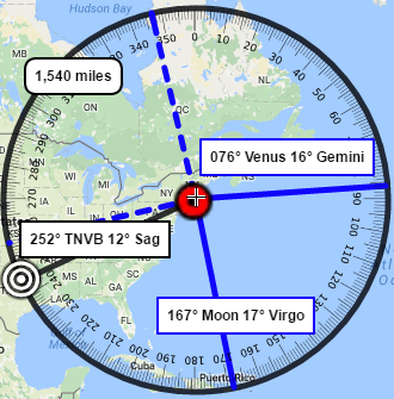
In the Matter of Direction
The compass bearing from the White House to downtown Dallas, Texas is 252° which is also expressed as 12° of Sagittarius.
In the Matter of Distance
It was 1504 Miles from JFK's point of birth to the point of Dallas, Texas where he was assassinating. If we add up JFK's planets in their total degrees of celestial longitude from the Sun to Pluto, include his Ascendant and Midheaven measurements it adds up to 1428, which is 76 less than 1504, the same measurement of his natal Venus, the planet that was positioned in his charts' house of death ---which if added to 1428 would equal 1504.
|
Abraham Lincoln |
16th President of the United States
|
|
In the Matter of DISTANCE
It was 483 Miles from the point of Lincolns' birth to the White House. Lincolns' Neptune at birth measured 246° which when inverted can become the number 462 leaving us just 21 short to the White House. But when you add in his ruler of the 10th House, Public Life, Jupiters' 22° measurement in Pisces gives us the extra we need to get us right to the White House.
In the Matter of Direction
|
The compass bearing from Hodgenville, Kentucky to the White House is 076° which is also expressed as 16° of Gemini. Both of
- Lincolns' natal Sun at 23° of Aquarius and his ASCendant @ 22° Aquarius Trine this point by 7 degrees, while his
- at 25° Libra Mars also trines this point by 9 degrees,
- but that old Planet of Death Pluto at his birth measured 13° of Pisces forms a Square to this point by 3 degrees.
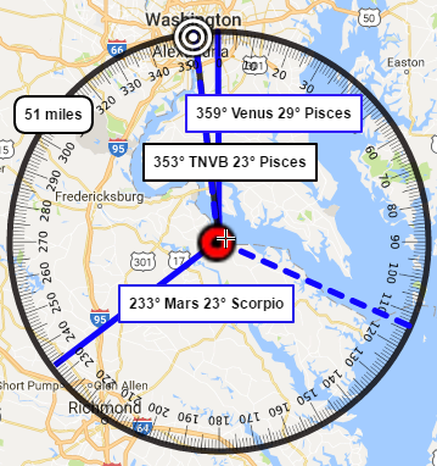
George Washington |
1st President of the United States
|
In the Matter of DISTANCE
It was 51 Miles from the point of Washingtons' birth to the White House. Washingtons' Ascendant was 18° of Taurus which also measures 048° of total celestial longitude. Washingtons' Saturn formed a semi-square to this point by its measurement of 002° at @° Aries. When you add the 2 to the 48 its sums to 51 offering the distance from his birth place to the White House.
In the Matter of DIRECTION
The compass bearing from Washingtons' birth place o the White House is 353° which is also expressed as 23° of Pisces.
Note: Don't you think its refreshing to learn that for Washington his own Planet of Death Pluto played no role is his destiny to the White House as it did in the lives of Kennedy and Lincoln who were both assassinated while US Preesidents as previously illustrated?
However, we can never escape our own natal Pluto. For Washington, he had his Pluto in the air sign of Libra. He died at home on the 14th of December, two days after becoming ill from spending the day outside in the elements on horseback tending to his plantation in snow, hail and freezing rain. Washingtons' Pluto @ 17° Libra formed a Triangle to his Neptune @ 14° Gemini , the planet of mystery. It remains today that Washington's cause of death is still a much debated subject.
- Washingtons' natal Venus conjoined this point at 29° of Pisces by 6 degrees, while and his
- Mars @ 23° Scorpio formed an exact Trine to this point.
Note: Don't you think its refreshing to learn that for Washington his own Planet of Death Pluto played no role is his destiny to the White House as it did in the lives of Kennedy and Lincoln who were both assassinated while US Preesidents as previously illustrated?
However, we can never escape our own natal Pluto. For Washington, he had his Pluto in the air sign of Libra. He died at home on the 14th of December, two days after becoming ill from spending the day outside in the elements on horseback tending to his plantation in snow, hail and freezing rain. Washingtons' Pluto @ 17° Libra formed a Triangle to his Neptune @ 14° Gemini , the planet of mystery. It remains today that Washington's cause of death is still a much debated subject.
In the Matter of DISTANCE
Bill Clinton |
42nd President of the United States
|
This Page is in Progress of adding more Presidents as we collect the data.